Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Enveloppe convexe

    Formulaire de report


    Enveloppe convexe \(\operatorname{Hull}(A)\) de \(A\subset E\) un Espace vectoriel Intersection de toutes les parties convexes de \(E\) qui contiennent \(A\).
    • c'est aussi le plus petit convexe contenant \(A\)
    • obtention : c'est l'ensemble des combinaisons convexes d'éléments de \(A\), i.e. \(y\in\operatorname{Hull}(A)\) si et seulement s'il existe \(p\geqslant1\), des éléments \(a_1,\dots,a_p\in A\) et \(t_1,\dots,t_p\) des nombres positifs de somme \(1\) tq \(y=t_1a_1+\dots+t_pa_p\)
      •     
    • théorème de Carathéodory : si \(X\subset{\Bbb R}^d\), alors \(\operatorname{Hull}(X)\) peut s'écrire comme l'ensemble des combinaisons convexes de \(d+1\) éléments de \(X\)
    • dans un evn ou un Espace affine de dimension finie, l'enveloppe convexe d'un compact est compact
    • si \(K\) est un compact d'un Espace de Banach, alors \(\operatorname{Hull}(K)\) est relativement compacte
      •     
    • si \(K\) est un compact de \({\Bbb R}^d\), alors \(\operatorname{Hull}(K)\) est compact


    Questions de cours

    START
    Ω Basique (+inversé optionnel)
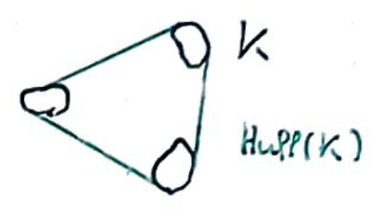
    Recto: Quelle est l'enveloppe convexe de trois points ?
    Verso: C'est le triangle formé par ces trois points.
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Quelle est l'enveloppe convexe de \(O_n({\Bbb R})\) ?
    Verso: C'est la boule unité fermée de \(M_n({\Bbb R})\) pour la Norme subordonnée à la norme euclidienne Bonus:
    Carte inversée ?:
    END
    Montrer que dans un Espace de Banach, l'enveloppe convexe d'un compact est relativement compacte.

    Pour tout \(n\in{\Bbb N}\), on pose on un ensemble compact de centres de boules de rayon \(\frac1n\) qui recouvrent \(K\).

    On prend une suite d'éléments dans l'enveloppe convexe, qu'on exprime comme combinaison convexe d'éléments de \(K\).

    Alors par construction des \(K_n\) il existe toujours un élément assez proche de \(x^k\).

    Le produit des enveloppes convexes de \(K_n\) est convexe par le Théorème de Tychonov, donc on peut extraire une sous-suite convergente des \((x^k_n)_k\).

    La suite ainsi formée et de Cauchy par construction, donc converge et donne le Critère de Bolzano-Weierstrass.


    START
    Ω Basique (+inversé optionnel)
    Recto: Donner l'expression de l'enveloppe convexe d'un ensemble \(X\subset{\Bbb R}^d\), en suivant le théorème de Carathéodory.
    Verso:

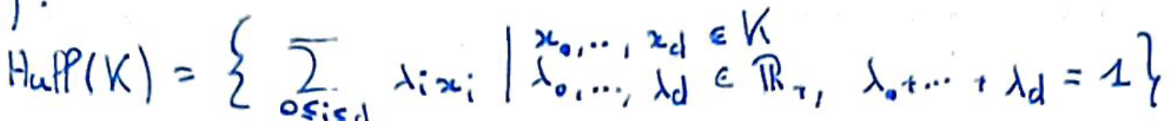
    Bonus:

    Carte inversée ?:
    END
    Démontrer :

    On pose l'ensemble des \((d+1)\)-uplets de nombres positifs qui peuvent former une combinaison convexe.

    C'est un fermé borné, donc un compact.

    L'enveloppe convexe est ainsi compacte en tant qu'image d'un produit de compacts par une application continue.


    Démonstration du théorème de Carathéodory :

    Par définition de l'enveloppe convexe, tout point peut s'écrire comme une combinaison convexe d'éléments de \(X\).

    On suppose \(I\) minimal \(\to\) si \(I\leqslant d\), alors c'est plié.

    Dans le cas contraire, la famille des \((x_i-x_0)_{i}\) est liée par argument de dimension.

    On peut donc prendre \(I\) coefficients \(\mu_i\) qui annulent la somme des \((x_i-x_0)\), et un dernier coefficient qui s'assure que \(\sum_i\mu_ix_i=0\).

    Alors la somme \(\sum_i(\lambda_i-t\mu_i)x_i\) est égale à \(x\) pour tout \(t\).

    En prenant \(t\) égal au ration maximal \(\frac{\mu_i}{\lambda_i}\), on peut alors exprimer \(x\) comme combinaison de \(I-1\) termes, ce qui contredit la minimalité de \(I\).




    Exercices

    START
    Ω Basique (+inversé optionnel)
    Recto: Montrer qu'en dimension finie, l'enveloppe convexe d'un Fermé n'est pas forcément fermée.
    Verso:

    Bonus: Théorème de Carathéodory Carte inversée ?:
    END
    Soit \(H\) un Espace de Hilbert de dimension infinie muni d'une base hilbertienne \((e_n)_n\).
    En considérant \(f_n=\frac{e_n}{n+1}\), montrer que l'enveloppe convexe d'un compact n'est pas toujours Fermés en dimension infinie.

    On considère l'union des \(f_n\), à laquelle on ajouté sa limite.

    C'est un compact d'après le Critère de Bolzano-Weierstrass.

    On pose \(x_n\) la somme des \(n\) premiers \(2^{-k}f_k\) à laquelle on a rajouté le dernier terme.

    C'est une combinaison convexe d'éléments de \(F\), qui de plus converge.

    Or \(x\) ne s'écrit pas comme combinaison convexe avec un nombre fini de termes, ce qui contredit la caractérisation séquentielle des fermés.




    \(A\) est bornée, donc contenue dans une boule.

    Comme la boule est convexe, elle contient l'enveloppe convexe de \(A\), qui est donc bornée (et donc de diamètre fini).

    On va montrer que les deux diamètres sont égaux par double-inégalité \(\to\) l'une est facile par inclusion.

    Pour l'autre inclusion, prendre un point dans l'enveloppe convexe et l'exprimer à l'aide du Théorème de Carathéodory.

    On peut utiliser cette expression et une \(\ne\!\!\!\triangle\) pour majorer la distance entre un point de \(A\) et \(x\).

    On peut ensuite majorer en utilisant le fait que les \(x_i\) sont dans \(A\) et que \(\lambda_1+\dots+\lambda_n=1\).


    On prend un autre point de l'enveloppe convexe, qu'on exprime également à l'aide du Théorème de Carathéodory.

    En faisant comme précédemment, on peut majorer la distance entre \(x\) et \(z\) par le diamètre \(A\).

    C'est valable pour tout couple de points de l'enveloppe convexe, ce qui nous permet de passer à la borne supérieure (points qui donnent le diamètre) et d'avoir la deuxième inégalité.